国考行测数量关系：相遇追及破题点

点击预约2023年国考&下半年四川省考,还可获取考情资料

在每一年的国考和省考的数量关系中，行程问题已经成为了必考的内容之一。行程问题又分为两类，一类是基础行程问题，另一类是相遇追及问题。行程问题中同学们一直存在的难点就是相遇追及问题，很多学生一直不明白，相遇和追及的距离怎么去寻找，以及在相遇追及中所花费的时间也把握不清楚。

在做题的过程中我们一定要首先读懂题干，明白这个题目是考查相遇问题还是追及问题，其次对于相遇问题要搞清楚相遇问题是两个人迎面走来相遇，所以相遇距离等于两人共同行驶的距离，故有公式为。追及问题是两人在同一方向运动，此时两人速度不同，且起始所处位置是一前一后，则两人起始相距的距离即为追及距离，也就是位置处于后面的人比位置处于前面的人多跑的距离，故有公式为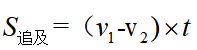。zui后，不论是相遇问题还是追及问题，都是花费相同的时间，才能够去使用公式，如果题目中出现时间不同时，可认为由一方先出发n小时，另一方再出发。要让两人在相遇行驶过程中的时间保持相等。接下来我们通过几个例题感知一下：

【例1】甲乙两车早上分别同时从A、B两地出发，驶向对方所在城市，在分别到达对方城市并各自花费一小时卸货后，立刻出发以原速返回出发地。甲车的速度为60千米/小时，乙车的速度为40千米/小时。两地之间相距480千米。两车第二次相遇距离两车早上出发经过了多少个小时?

A.13.4

B.14.4

C.15.4

D.16.4

【答案】C

【正确率】

【三级知识点】数量关系-数学运算-行程问题-相遇追及类

【例2】甲、乙两辆汽车从A地出发，同向而行，甲每小时走45千米，乙每小时走60千米。若甲车比乙车早出发2小时，则乙车追上甲车需要( )。

A. 6小时 B. 7小时

C. 8小时 D. 9小时

【答案】A

【解析】

第*步：本题考行程问题中的追及问题。

第二步：假设乙车追上甲车需要t小时，则根据追及问题的公式可得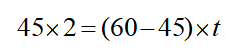，解得t=6。

因此，选择A选项。

【例3】某周末，甲、乙约好在两人之间的某商店碰面，已知甲走路的速度为4km/h，乙走路的速度为3km/h，两人同时出发，zui终同时到达相遇地点，已知甲、乙两地相距7km，则该商店距离甲( )。

A. 3km B. 4km

C. 5km D. 6km

【答案】B

【解析】

第*步：本题考查行程中的相遇问题。

第二步：假设相遇需要的时间为t，由相遇问题公式可得，则可得7=(3+4)t，解得t=1，则该商店距离甲的距离为甲走的路程4*1=4。

因此，选择B选项。

以上几个例题会发现，在不论是相遇问题还是追及问题，找到相遇和追及距离以及在相遇追及过程中所花费的时间是我们破题的关键所在。

 

　　国考推荐

　　历年入面分数 知识大普及 数读国考国 考空间站

　　国考问答百科 报考指导 国考时间轴 申论备考

　　国考行测备考 图书网课备考 公安联考公告预约

（编辑：Nicj）