四川公务员关于四川2021年公务员考试时间(3)

预约享全项目备考资料

　　言语如何备考》》》

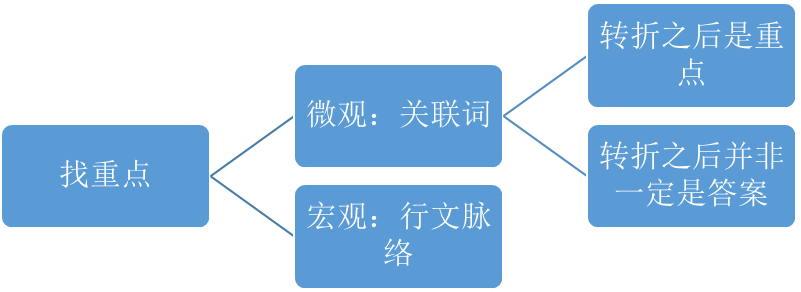
　　国联考中关于言语模块的测查，转折这个知识点一直是重点考察的对象。但大多同学在学习的过程中存在理解偏差，以偏概全。认为转折就是解题的不二法门，将转折之后是重点和转折之后是答案划等号。这其实是非常错误的理解，关联词只能体现关联词词前和词后的关系，转折前和转折后作比较，转折后是重点。但是不是答案，还需要比对转折后和其他句子的关系。所以各位同学在寻找文段重点句的过程中切忌只找关联词，还是应当将微观与宏观相结合。如此才能精准寻找全文重点句。

　　例1. 夏日高温炎热，水成为消暑的必备品。但对开车一族而言，久置在高温、闷热车厢里的饮料是健康的潜在威胁。用塑料制成的饮料瓶，用一次是安全的，如果重复使用就有致癌危险。这些饮料瓶在室温下，可保存较长时间，但若经阳光暴晒，就会发生材质老化、释放出有毒物质，人饮用瓶内的饮料后会出现恶心、呕吐等慢性中毒反应。

　　这段文字主要说明的是：

　　A. 夏季如何避免车内饮料变质

　　B. 一次性饮料瓶含有致癌物质

　　C. 司机在夏季开车要及时补充体内水分

　　D. 夏季久置车厢内的饮料是健康的潜在威胁

　　解析：文段首先给出但是这一转折词，可以判定，与第*句话作比较重点在转折之后。但阅读后文即可发现，文段倒数第*句话也存在转折词但是。两者作比较会发现，第二个转折是对第*个转折的解释说明。故此认为全文重点在第*个转折句之上。答案也就唯一，选择D答案，无可争议。

　　例2. 文化时尚总是从一种文明传到另一种文明，一种文明中的革新常被其他文明所采纳。然而，它们往往只是一种缺乏重要文化后果的技术或昙花一现的时尚，并不会改变文明接受者的基本文化。西方世界曾经出现渴慕来自中国或印度文化的各种物品的热潮;而在19世纪的中国和印度，来自西方的通俗文化和消费品流行起来，似乎代表着西方文明的胜利。然而，这种“流行”恰恰使西方文化变得无足轻重。西方文明的本质是“大宪章”而不是“巨无霸”，非西方人可能接受后者，但这对于他们接受前者来说没有任何意义。

　　对这段文字的观点概括zui准确的是：

　　A. 人们常出于猎奇心理而接受来自异域的东西

　　B. 不同文化之间很难实现本质上的交流与影响

　　C. 西方和非西方世界在文明的本质上存在差异

　　D. 时尚的传播不会根本改变接受者的基本文化

　　解析：此题首先给出转折词“然而”，可以体会出，然而前和然而后作比较重点在然而之后。可如此就能贸然仍定它就是全文重点吗，答案是否定的。阅读后文会发现，倒数第二句话也提到了然而一词，也构成了转折。那么重点到底在哪个句子之上，可以发现，第二个转折句描述话题西方文化，相比较于前者文化这一话题而言，话题在走向具体，属于例子表达，故认为第二个转折属于例子内部转折，不重要。重点句在第*个转折之后，答案唯一，选择D答案，无可争议。

　　由以上两题可以看出，其实转折词的应用非常广泛，但是各位同学在使用过程中一定要学会擦亮双眼，通读全文，把握重点，而非唯转折是从。

　　

　　判断如何备考》》》

　　2022国考行测备考技巧巧用隔板法解决排列组合问题

　　行测中，数量关系考察大家对于各种题型的掌握及快速解题的能力，是大家zui为头疼的一个模块。数量关系题目变化虽复杂，但并不是没有规律可循的。事实上，数量关系模块中的技巧性是很强的，要想快速提升分数，就需要大家掌握一些实用技巧。在排列组合中有一类将几个相同元素分给若干个人的题型，大家虽都有一个固定的套路去解题，但是比较耗费时间。在此，给大家介绍一个非常实用的技巧快速解题。

　　题目情境：

　　把m个相同的元素分给n个不同的对象，每个对象至少分得1个，一共有多少种不同的分法?

　　题目特点：

　　m个元素是完全相同的，并且将元素全部分完。

　　每个对象至少分一个。

　　结论：

　　共有种分法。

　　接下来，通过例题为大家展示一下如何运用。

　　典型例题：

　　【例1】有10个完全相同的玩具车，分给3个不同的小朋友，每个小朋友至少分得1个玩具车，问有多少种不同的分配方案?

　　A.32 B.36

　　C.72 D.48

　　【答案】B

　　【解析】解法一：常规解法。根据条件，将10个玩具车分成3堆，分给小朋友，共有：

　　1，1，8;分给3个人，共有3种分法。

　　1，2，7;分给3个人，共有6种分法。

　　1，3，6;分给3个人，共有6种分法。

　　1，4，5;分给3个人，共有6种分法。

　　2，2，6;分给3个人，共有3种分法。

　　2，3，5;分给3个人，共有6种分法。

　　2，4，4;分给3个人，共有3种分法。

　　3，3，4;分给3个人，共有3种分法。共计36种。

　　解法二：隔板法。观察题干，符合隔板法使用要求。第*步，把10个玩具车分成3堆，需要隔2个板;第二步，10个玩具车共形成11个空(加上左右两边两个空)，但不可以把板放在zui边上的空里，也不可以把两个板放到一个空里，故需要在中间9个空中选2个放入板子，即：，(注：在此过程中，无需再考虑顺序)。因此，本题的答案为B选项。

　　【例2】有30个苹果，分给4个不同的小朋友，每个小朋友至少分得4个苹果，问有多少种不同的分配方案?

　　A.540 B.680

　　C.1360 D.1456

　　【答案】B

　　【解析】题干中，不符合隔板法第二个使用要求“每个对象至少一个”，可进行转化：每个小朋友每人先给3个苹果，即可替换为：18个苹果分给4个小朋友，每个小朋友至少分1个苹果，有多少种分法?就是在17个空中插3个板 ：。因此，本题答案为B选项。

　　【例3】某单位圣诞节准备了8份相同的礼物，打算分给4名员工中的一名或多名，请问有多少种不同的分法?

　　A.35 B.84

　　C.165 D.330

　　【答案】C

　　【解析】题干中，将8份相同的礼物分给4名员工，但是题干中并没要求每人至少分一份，因此可以构造“至少分一份”，然后再使用隔板法。假设先向每人借一份，此时共有礼物8+4=12(份)，这12份相同的礼物再分给4名员工时每人至少分一份(将借的一份还了)，就是在11个空中插入3个板，共有 =165(种)分配方式。因此，本题选择C选项。

　　通过三个典型例题，大家不难发现，隔板法是一类技巧性很强的排列组合问题的解决方法。不管是针对简单的模型题目还是针对变型模型，大家只要记住隔板法的应用条件，若是不符合条件，将其转化之后再应用即可。

　　河北分院

　　

（编辑：Nicj）