2025河北国家公务员考录专题网http://www.scs.gov.cn/

2025河北国家公务员考录专题网http://www.scs.gov.cn/由四川华图国家公务员考试网整理分享,更多关于国家公务员招聘公告,四川国考岗位表,国家公务员报考相关的内容，请关注四川国家公务员考试网！

　　2025河北国家公务员考录专题网？2025年全国公务员考试公告暂未发布，按照历年的考情时间来预计在10月中旬发布公告，11月底笔试。准备25国考的考生请参照下文时间进行备考：

　　25国考公告预约：https://sc.huatu.com/zt/25gkggyy/?25gjc

　　国考历年公告：https://sc.huatu.com/zt/gjgwy/?25gjc

　　国省考历年真题：https://sc.huatu.com/zt/lnzt/?25gjc

　　国省考历年分数线：https://sc.huatu.com/zt/gwyfsx/?25gjc

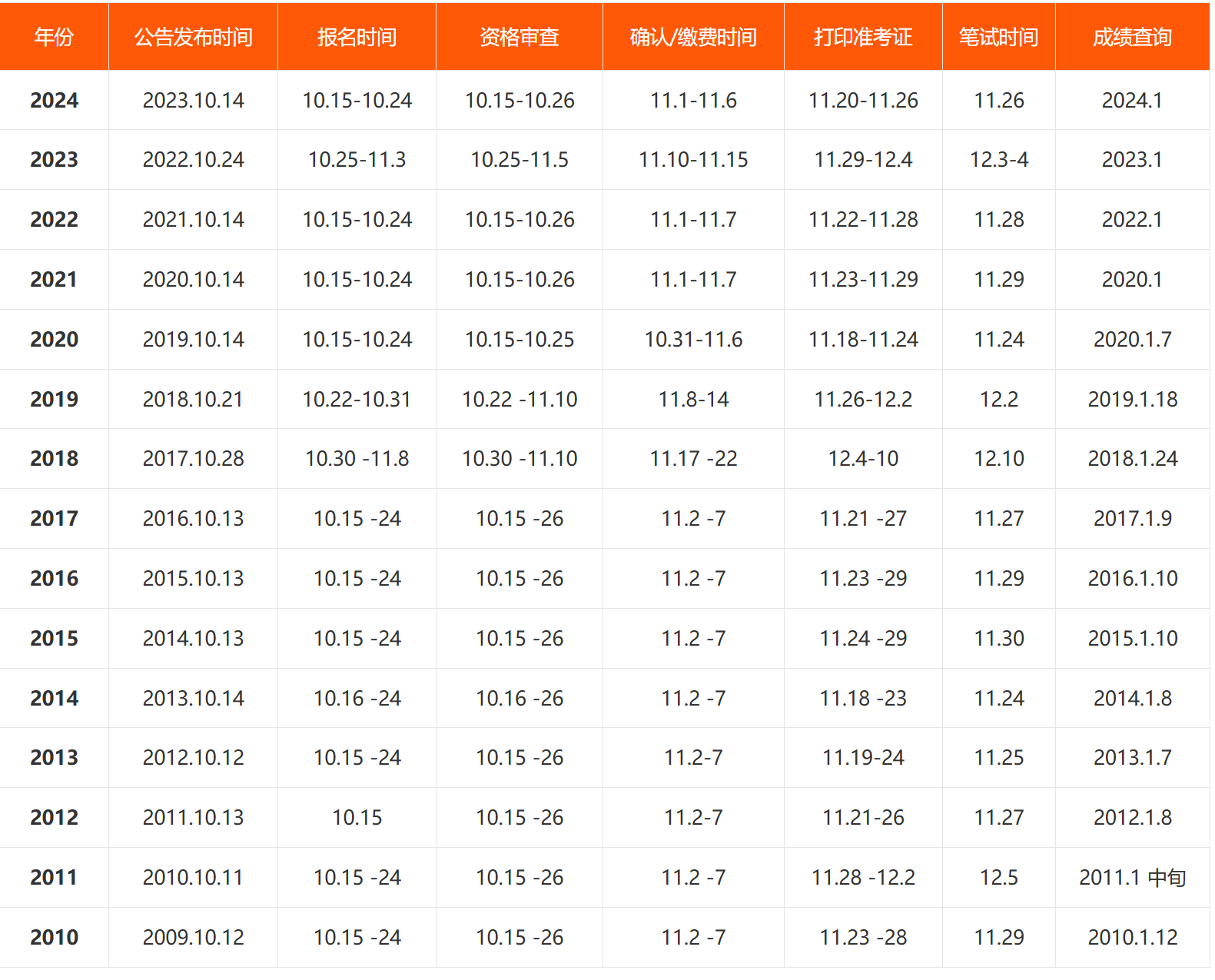
　　一、参加全国联考的省份有哪些

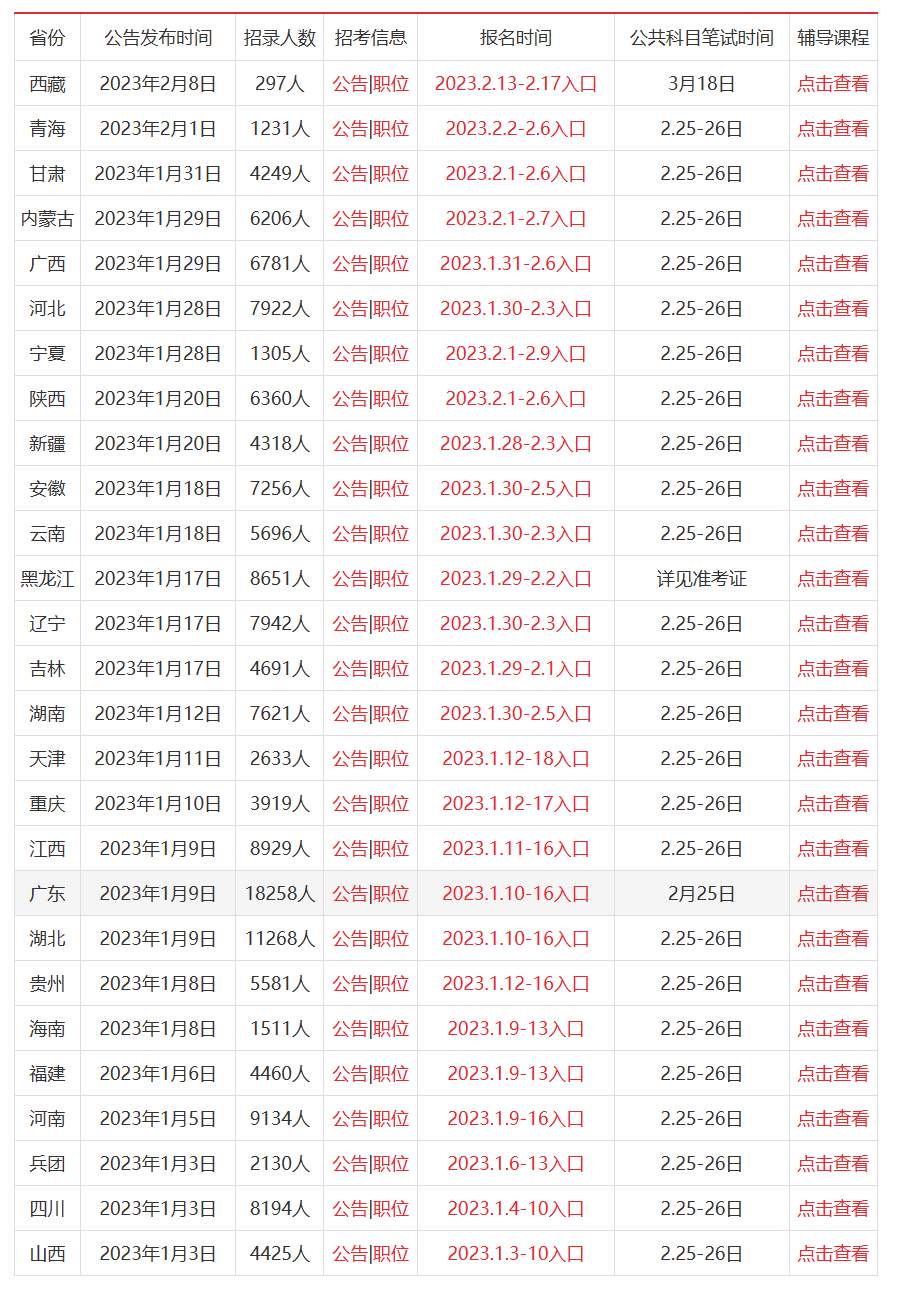
　　按照历年全国公务员的招考情况，参加全国联考的省份有青海、甘肃、内蒙古、广西、河北、宁夏、陕西、新疆、安徽、云南、黑龙江、辽宁、吉林、湖南、天津、重庆、江西、广东、湖北、贵州、海南、福建、河南、兵团、山西，以下是2023年全国公务员的重要时间表和招录人数汇总。

　　三、报名程序（以2024年招考公告为例参考使用）

　　(一)网络报名

　　报考者应在2024年1月8日9:00至1月12日17:00登录福建考录网完成报名手续。本次考试不收取报名费，报考者应通过“闽政通APP”L4级身份认证后，方可提交报考申请。

　　本次考试在各设区市设置考场。报考者(含加考公安基础知识)可自行选择考区参加笔试。报考需要加试其他专业科目职位的，只能选择福州考区参加考试。1月19日24:00后，报考者不得修改笔试地点。

　　(二)查询初审结果

　　报考者可在报名次日起2个工作日后，登录福建考录网查询初审结果。每个报考者成功报考1个职位后，不得改报其它职位。

　　(三)申诉审核

　　1月9日9:00至1月15日17:00，报考者与招录单位沟通后，对“专业资格不符”结论仍有异议的，可及时通过网络报名系统的申诉通道对专业资格提出复审申请，由公务员主管部门进行认定。

　　(四)笔试确认

　　1月17日9:00至1月19日24:00，通过资格审查的报考者应登录福建考录网完成笔试确认手续，未按规定时间完成确认的，视为放弃考试资格。

行测数量关系中有一种看似简单却暗藏玄机的题型——容斥问题，今天跟着四川华图一起来揭开“她”神秘的面纱。

一、知识铺垫

容斥问题研究的是集合之间的交叉关系，对于容斥问题的解题原则，我们总结了四个字：“不重不漏”，即“每个区域的元素只算一次”。

如图(1)所示，A、B两个集合之间的交叉关系为二者容斥问题，“不重不漏”就是把①、②、③及M四个区域各算一次，总结为公式：如图(2)所示，A、B、C三个集合之间的交叉关系为三者容斥问题，同理“不重不漏”就是把①-⑦及M八个区域各算一次，总结为公式：接下来我们通过两道例题加以理解。

二、例题展示

例1、工厂组织职工参加周末公益劳动，有80%的职工报名参加。其中报名参加周六活动的人数与报名参加周日活动的人数比为2：1，两天的活动都报名参加的人数为只报名参加周日活动的人数的50%。问未报名参加活动的人数是只报名参加周六活动的人数的：

A.20% B.30% C.40% D.50%

【答案】C

【解析】设两天的活动都报名参加的人数为x，则只报名参加周日活动的人数为2x，由“报名参加周日活动的人数等于两天的活动都报名参加的人数与只报名参加周日活动的人数之和”，可得报名参加周日活动的人数为3x，根据“报名参加周六活动的人数与报名参加周日活动的人数比为2：1”，可得报名参加周六活动的人数为6x，从而只报名参加周六活动的人数为5x，那么报名参加活动的总人数为：2x+5x+x=8x，由于“有80%的职工报名参加”，所以工厂职工总数为：8x÷80%=10x，那么未报名参加活动的人数为：10x-8x=2x，所求是：2x÷5x=40%。故答案选C。

例2、有100人参加运动会的三个比赛项目，每人至少参加一项，其中未参加跳远的有50人，末参加跳高的有60人，未参加赛跑的有70人。问至少有多少人参加了不止一个项目?

A.7 B.10 C.15 D.20

【答案】B

【解析】根据“有100人参加运动会的三个比赛项目，每人至少参加一项”可知这100人中没有不参加运动会的人，由“其中未参加跳远的有50人，末参加跳高的有60人，未参加赛跑的有70人”可分别得出：参加跳远的有50人，参加跳高的有40人，参加赛跑的有30人。设参加两项的有x人，参加三项的有y人，根据三者容斥公式可得：50+40+30-x-2y=100，解得x+2y=20。所求为：“至少有多少人参加了不止一个项目”，即求的是x+y的最小值。由x+y=20-y，可知要想求出x+y的最小值，就要使y尽可能大，当x为0时，y取最大值为10，所以求出x+y的最小值是：20-10=10。故答案选B。

通过这两道例题我们可以发现只要分析好题干中各个集合所代表的具体含义