国家公务员报名时间不多了，还在观望的考生可以开动了——这个阶段报名人数每日都在激增，我们来看看四川眉山市地区的报名情况：2022年国家公务员在眉山市地区招录42个职位，总共44人。截止 10月22日11：00 眉山市地区已经报名2793人，其中待审核407人,审核通过2386人。整个眉山市地区的国家公务员报考竞争比已经达到了66: 1。下面是具体数据
| 截止10月22日11：00 ，眉山市地区国家公务员报名数据 | ||||||
| 地区 | 职位数 | 招录人数 | 报名人数 | 待审核人数 | 审核通过 | 竞争比 |
| 四川省 | 895 | 1237 | 48680 | 7019 | 41661 | 54: 1 |
| 眉山市 | 42 | 44 | 2793 | 407 | 2386 | 66: 1 |
根据上表可以看到，截止10月22日11：00 ，全四川已经报名了48680人，其中，眉山市地区报名了2793人。另外国家公务员眉山市地区的岗位在整个四川来看是属于报考竞争比较激烈的岗位，因为其竞争比为66: 1大于四川省所有岗位的平均竞争比54: 1。zui后提醒，本次国家公务员报名时间即将于10月24日18:00结束，届时报名入口将自动关闭，各位考生需要尽快在国考报名系统去报名，另外，报名后记得缴费！！
国家公务员备考资料>>>>
2022国考行测备考技巧巧用隔板法解决排列组合问题
行测中，数量关系考察大家对于各种题型的掌握及快速解题的能力，是大家zui为头疼的一个模块。数量关系题目变化虽复杂，但并不是没有规律可循的。事实上，数量关系模块中的技巧性是很强的，要想快速提升分数，就需要大家掌握一些实用技巧。在排列组合中有一类将几个相同元素分给若干个人的题型，大家虽都有一个固定的套路去解题，但是比较耗费时间。在此，给大家介绍一个非常实用的技巧快速解题。
题目情境：
把m个相同的元素分给n个不同的对象，每个对象至少分得1个，一共有多少种不同的分法?
题目特点：
m个元素是完全相同的，并且将元素全部分完。
每个对象至少分一个。
结论：
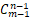种分法。
接下来，通过例题为大家展示一下如何运用。
典型例题：
【例1】有10个完全相同的玩具车，分给3个不同的小朋友，每个小朋友至少分得1个玩具车，问有多少种不同的分配方案?
A.32 B.36
C.72 D.48
【答案】B
【解析】解法一：常规解法。根据条件，将10个玩具车分成3堆，分给小朋友，共有：
1，1，8;分给3个人，共有3种分法。
1，2，7;分给3个人，共有6种分法。
1，3，6;分给3个人，共有6种分法。
1，4，5;分给3个人，共有6种分法。
2，2，6;分给3个人，共有3种分法。
2，3，5;分给3个人，共有6种分法。
2，4，4;分给3个人，共有3种分法。
3，3，4;分给3个人，共有3种分法。共计36种。
解法二：隔板法。观察题干，符合隔板法使用要求。第*步，把10个玩具车分成3堆，需要隔2个板;第二步，10个玩具车共形成11个空(加上左右两边两个空)，但不可以把板放在zui边上的空里，也不可以把两个板放到一个空里，故需要在中间9个空中选2个放入板子，即：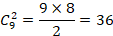
，(注：在此过程中，无需再考虑顺序)。因此，本题的答案为B选项。
【例2】有30个苹果，分给4个不同的小朋友，每个小朋友至少分得4个苹果，问有多少种不同的分配方案?
A.540 B.680
C.1360 D.1456
【答案】B
【解析】题干中，不符合隔板法第二个使用要求“每个对象至少一个”，可进行转化：每个小朋友每人先给3个苹果，即可替换为：18个苹果分给4个小朋友，每个小朋友至少分1个苹果，有多少种分法?就是在17个空中插3个板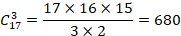
：。因此，本题答案为B选项。
【例3】某单位圣诞节准备了8份相同的礼物，打算分给4名员工中的一名或多名，请问有多少种不同的分法?
A.35 B.84
C.165 D.330
【答案】C
【解析】题干中，将8份相同的礼物分给4名员工，但是题干中并没要求每人至少分一份，因此可以构造“至少分一份”，然后再使用隔板法。假设先向每人借一份，此时共有礼物8+4=12(份)，这12份相同的礼物再分给4名员工时每人至少分一份(将借的一份还了)，就是在11个空中插入3个板，共有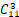
＝165(种)分配方式。因此，本题选择C选项。
通过三个典型例题，大家不难发现，隔板法是一类技巧性很强的排列组合问题的解决方法。不管是针对简单的模型题目还是针对变型模型，大家只要记住隔板法的应用条件，若是不符合条件，将其转化之后再应用即可。
国考推荐
（编辑：Nicj）
贴心微信公众号
四川公务员微信群
点击预约2023年国考&下半年四川省考,还可获取考情资料
